Rotating objects in 3D Engines
Rotating Objects
We frequently rotate objects using 3D Engines. I’m sharing some rotating algorithms with descriptions based on
mathematical theorems.
Note that there could be lots of ways to do it, though.
1. Object rotated in 3D space by mouse drag motion on 2D display screen.
Assume that the user wants to rotate an object by mouse drag on the screen.
It means that we have to rotate the object with two specific mouse position of the screen,
on click down and on drag. Assume that a transform matrix of the camera is also fixed for convenience.
Then the mouse drag motion with an object would be like this.
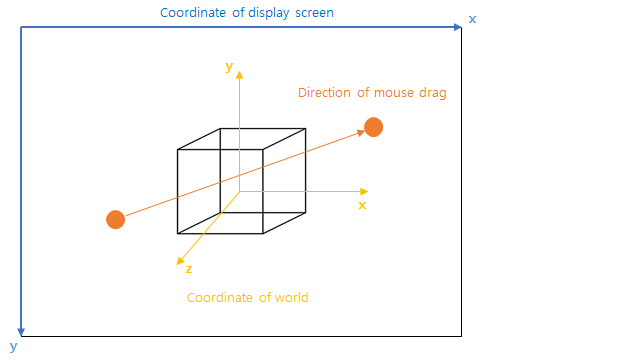
A circle left one is a starting point of the drag(on click down), and the right one is the last position of on drag at the frame. Then, we can suppose that the user wanted to rotate the box(object) by right-top direction with the amount of drag length. It means that we have to translate those points of display space into world space positions.
1) Let define P=(x, y) and P’=(x’, y’), when dragging on the display screen P → P’.
Then, the size of the angle can be a scalar value of MouseDirection M = P’ - P.
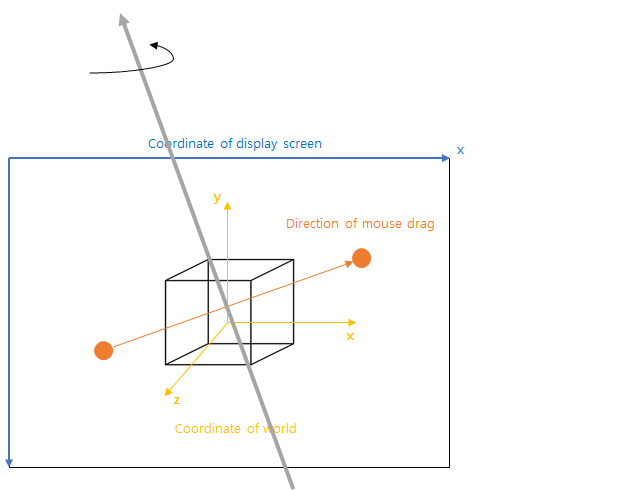
2) Assume that the fixed camera is positioned at (0, 0, a > 0) to show the object.
Then, we can get an axis by the cross product of the M and direction of the camera ‘LookAt’
vector (0, 0, -a) like below image.
Finally, we got both an angle and an axis from this model. Create a rotation quaternion by this angle-axis and rotate the object.
Source code would be like this.
@Override
public void onDown(MouseEvent e, Object o) {
// get previous orientation of the object on click-down.
prevOrientation = o.get().getTransformData().getOrientation();
// get mouse click-down position.
prevX = e.x;
prevY = e.y;
}
// Note: Canvas defines right direction as +x, down direction as +y.
@Override
public void onDrag(MouseEvent e, Object o) {
// Calculate P' - P = (dx, dy) = delta
int dx = e.x - prevX;
int dy = e.y - prevY;
Vector3f delta = new Vector3f(dx, -dy, 0);
// Angle
float angle = delta.length();
// Axis: find axis of the rotation. (0, 0, -1) is just a position of fixed camera for this calculation.
Vector3f rotAxis = new Vector3f(0, 0, -1).cross(delta).normalize();
// Create and apply the rotation to previous object's orientation and set this orientation to the object.
Quaternionf rotation = new Quaternionf(new AxisAngle4f(angle, rotAxis));
Quaternionf newOrientation = new Quaternionf(prevOrientation).mul(rotation);
// This newOrientation could be replaced by rotation * prevOrientation as needed.
o.get().getTransformData().setOrientation(newOrientation);
}
This mechanism will work well. But, If you tried using local based rotation as the above code, you may realize that it is a little hard to rotate the object properly if the angle of any axis reached over 180 degrees. That’s because the object is turned over. Rotating reversed orientation of the object wouldn’t be intuitive because of the fixed camera view matrix.
This rotating local based way is for first-person’s camera view like FPS game. But, we’ve assumed to use the fixed camera like third-person’s camera view. So, let’s try the next solution.
2. The orbital rotation of camera by mouse drag motion
We are going to rotate the camera, not the object this time. Showing objects on every drag event on the display screen can be transformed by the camera view matrix, too. Imagine what should be done after the drag operation. Maybe the user wants to look around on the sphere. It is actually same as The Google Earth.
To do this, we have to get an orthogonal basis of the camera matrix first, because we would rotate the camera orientation based on the local coordinate system of the camera. Then, we can create a new rotation and apply the rotation with the previous solution based on this orthogonal basis.
1) Orthogonal basis of Camera
The camera LookAt is generally defined using two parameters, up vector and look at position data like below.
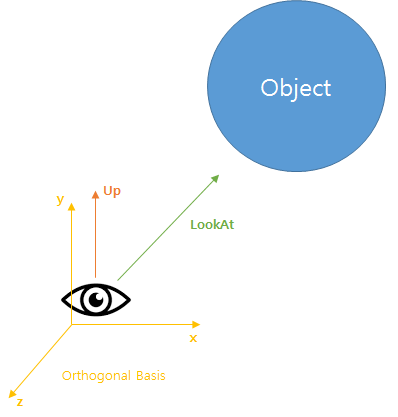
up vector(red arrow) indicates a direction of UP on the display screen, and look at vector indicates what the camera shows on the center of the display screen. According to this definition, up vector and look at vector can be perpendicular. So, we are now able to get the orthogonal basis.
Let define a vector O(x,y,z) which is the orthogonal basis of the camera, U is up vector and L is a look at vector.
Then,
$ O.z = -L $
$ O.y = U $
$ O.x = cross(L, U) $
Since the display screen shows based on the camera, every all data on mouse event should be translated to camera view based data. In other words, it’s based on the orthogonal basis. *(1)
2) Applying the rotation to the camera
In the previous solution, we’ve found the way to get the rotation by angle and axis data from on drag event. Hence, we can get the new rotation based on the orthogonal basis in the same way. It is time to apply the new rotation to the camera.
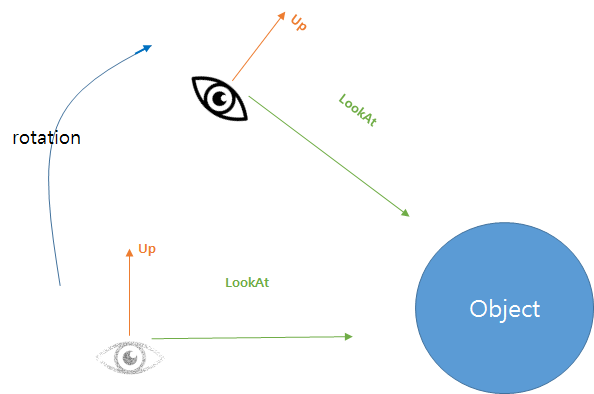
In this figure, you can see the camera is moved to a new position with its orientation, updating up vector. LookAt vector is also updated, but it will be done by only updating the position.
Source code would be like this.
@Override
public void onDown(MouseEvent e, TransformCamera camera) {
// get previous transform data of the camera on click-down
// calculating normalized orthogonal basis.
prevCameraBasis = camera.getOrthonormalBasisOrientationBase();
prevCameraTransform = camera.getTransformData().getCurrentTransformMatrix();
prevPosition = camera.getTransformData().getPosition3f();
prevX = e.x;
prevY = e.y;
}
@Override
public void onDrag(MouseEvent e, TransformCamera camera) {
Point delta = new Point(e.x - prevX, -(e.y - prevY));
// *(1) translate mouse data on screen to world space based on camera orthonormal basis.
Vector3f dx = new Vector3f(prevCameraBasis[0]).mul(delta.x);
Vector3f dy = new Vector3f(prevCameraBasis[1]).mul(delta.y);
Vector3f direction = new Vector3f(dx).add(dy);
// getting angle-axis for rotation same as previous solution.
float angle = direction.length();
Vector3f rotAxis = new Vector3f(direction).cross(prevPosition).normalize();
Quaternionf rotation = new Quaternionf(new AxisAngle4f(angle, rotAxis)).normalize();
// calculates new transform of the camera matrix by updating position and orientation.
Matrix4f transform = TransformData.getOrbitalRotationLookup(prevCameraTransform, zero, rotation);
camera.setTransformData(transform);
}
// TransformData#getOrbitalRotationLookup
public static Matrix4f getOrbitalRotationLookup(Matrix4f xForm, Vector3f center, Quaternionf rotation) {
// gets up vector and position from the matrix.
TransformData data = new TransformData(xForm);
Vector3f newPosition = data.getPosition3f();
Vector4f up = new Vector4f();
data.getCurrentTransformMatrix().getColumn(1, up);
Vector3f newUpVector = new Vector3f(up.x, up.y, up.z);
// rotate camera position and up vector
newPosition = rotation.transform(newPosition.sub(center));
newUpVector = rotation.transform(newUpVector);
// update look at vector.
Matrix4f ret = new Matrix4f();
ret.setLookAt(newPosition, center, newUpVector);
ret.invert(); // to view matrix
return ret;
}
Finally, let’s go back to the first solution and consider the rotation in the context of a movable camera.
3. Rotating objects based on the movable camera view
We’ve figured out the way to rotate object based on fixed camera view. But, it is necessary to transform the camera view. So, We’re going to find out the way to rotate the object right way even if the camera view is deformed.
Previously we’ve found rotation data by angle-axis from mouse drag, and It was a rotation data in the world coordinate system(WCS). That’s why we fixed the camera at (0, 0, -a). This position is on the z-axis, so we’re able to get the rotation data in WCS. We’re now going to transform the rotation data in WCS to CCS because the display screen would show objects in CCS from now on, not WCS anymore.
Remind that
1) rotation R in WCS by $ R = x_w * o $, where $ x_w $ is a rotation matrix to rotate it in WCS and o is the object to be rotated.
2) rotation R in WCS by $ R = o * x_l $, where $ x_l $ is a rotation matrix to rotate it in LCS.
Let define $ R = x_w * v $, where R is a result matrix of the rotation, v is the camera matrix. It means that R is the result rotated by $ x_w $ based in CCS (since we multiplied v to the right side). Definitely, we’re able to get the same R-value with $ x_l $ if we do rotate the camera (view) by local rotation formula. We can find the $ x_l $ to get the same R-value by above 1) and 2).
\(R = x_w * v = v * x_l\)
So, \(x_l = v^{-1} * x_w * v\)
$ x_l $ value now can be denoted by $ x_v $ that indicates the rotation in CCS since ‘local’ is now ‘camera’.
Hence, $ x_v = v^{-1} * x_w * v $.
Finally, we use the rotation in WCS formula again, $ R = x_w * o. $ (you can also apply the rotation in LCS here, too.)
// (SAME AS ABOVE SOLUTION 1.)
// Note that object for rotation is cube map in this code
@Override
public void onDown(MouseEvent e, GLPreview preview) {
prevOrientation = TypeConverter.FloatArrayToQuaternionf(preview.getCubemap());
prevX = e.x;
prevY = e.y;
}
@Override
public void onDrag(MouseEvent e, GLPreview preview) {
int dx = e.x - prevX;
int dy = e.y - prevY;
Vector3f delta = new Vector3f(dx, -dy, 0);
// Sets rotated orientation.
float angle = delta.length() / CAM_SENSITIVITY;
Vector3f rotAxis = new Vector3f(0, 0, -1).cross(delta).normalize();
Matrix4f rotationMat = new Matrix4f().set(new AxisAngle4f(angle, rotAxis));
/** ADDED SOLUTION HERE **/
// Get x_v from x_w and view matrix.
Matrix4f viewMatrix = new Matrix4f().set(mCamera.getViewMatrix());
Matrix4f viewMatrixInv = new Matrix4f(viewMatrix).invert();
rotationMat = viewMatrixInv.mul(rotationMat).mul(viewMatrix); // x_v
Quaternionf rotationCameraBased = new Quaternionf();
rotationMat.getUnnormalizedRotation(rotationCameraBased);
/** ADDED SOLUTION HERE END **/
Quaternionf newOrientation = rotationCameraBased.mul(new Quaternionf(prevOrientation)); // x_w * o
mPreviewCanvas.setCubemap(TypeConverter.quaternionfToFloatArray(newOrientation));
if(!mPreviewCanvas.isDisposed()) {
mPreviewCanvas.redraw();
}
}
You will be able to rotate the object freely by mouse drag under any camera, same as the result of orbital rotation.